Dinicov algoritam
Dinicov algoritam je strogo polinomijalni algoritam za izračunavanje maksimalnog protoka kroz transportnu mrežu osmišljen 1970. godine od strane izraelskog (prethodno sovjetskog) izučivača kompjutera Jefim Dinitz[1][1] algoritam se izvršava u vremenskom periodu O(V2E) i sličan je Emond-Karp Algoritmu koji se izvršava u vremenu O(VE2) u tome da koristi najkraće promenjene putanje. Uvod koncepta o grafa sa nivoima i blokiranja toka omogućuju Dinicovom algoritmu da postigne svoje izvođenje.
Istorija
[uredi | uredi izvor]Dinitc algoritam je 1970. godine objavio bivši ruski izučivač kompjutera Jefim A. Dinitc, koji je danas član Odseka za nauku računarstva na Ben-Gurion Univerzitetu Negav (Izrael), pre Edmonds-karp algoritma koji je objavljen 1972. godine ali je ranije otkriven. Nezavisno su pokazali da u Ford-fulkerson algoritmu[2][2] ako je svaka promenjljiva putanja najkraća, onda dužina promenljivih putanja ne opada.
Definicija
[uredi | uredi izvor]Neka je mreža sa i težina i protok grana (u tom redosledu).
- Preostala težina je Slikanje definisano kao
- 1. ako
- 2. inače
- 1. ako
- Preostali graf gde:
- Promenjljiva putanja je putanja u preostalom grafu .
- definišemo dist(v) da bude dužina nakraće putanje od s do v u grafu . Onda graf sa nivoima je graf gde:
- Blokirajući tok je tok takav da graf sa ne sadrži putanju
Algoritam
[uredi | uredi izvor]Dinicov algoritam
- Ulaz graf
- Izlaz: tok maksimalne vrednosti
- inicijalizujemo za svako
- Konstruišemo uz pomoć od . Ako je stani i stavi na izlaz.
- Nađemo blokirajući tok u
- Uskladimo uspomoć i vratimo se na drugi korak
Analiza algoritma
[uredi | uredi izvor]Može biti pokazano da se broj grana u svakom blokirajućem toku povećava za barem 1 svaki put tako da ima najviše blokirajućih tokova u algoritmu, gde je broj čvorova u grafu. Graf sa nivoima može biti konstruisan pretragom u širinu u vremenu a blokirajući tok u svakom nivou grafa se može pronaći u vremenu. Dakle Vreme izvršavanja ovog algoritma je .
Koristeći strukturu podataka zvanu dinamičko drve vreme potrebno za nalaženje blokirajućeg toka se može smanjiti na , pa se vreme izvršavanja ovog algoritma može poboljšati na .
Specijalni slučajevi
[uredi | uredi izvor]U grafu sa jediničnim težinama, postoji mnogo jača vremenska granica. Svaki blokirajući tok se može naći za i može se pokazati da broj faza ne prelazi i . Tako da se algoritam izvršava u vremenu[3].
U grafovima nastalim tokom rešavanja problema bipartitivnog uparivanja broj faza je ograničen sa , odtle vodeći vremensku granicu . Rezultujući algoritam je poznat kao Hopcrtft-Karp algoritam. Generalnije ova granica drži bilo koji graf -- graf u kojem svaki čvor osim izvora i ponora ima ili jednu ulaznu granu težine jedan ili jednu izlaznu granu težine jedan, a sve ostale težine su proizvoljni celi brojevi.[4]
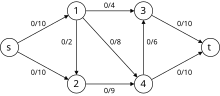
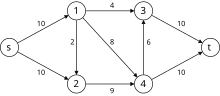
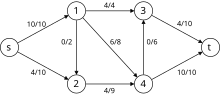
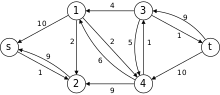
Primer
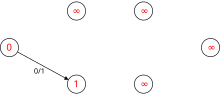
[uredi | uredi izvor]Sledeće je simulacija dinitc algoritma. U gafu sa nivoima čvorovi u crvenoj boji su vrednosti . Putanje plave boje su blokirajući tok.
Vidi još
[uredi | uredi izvor]Reference
[uredi | uredi izvor]- ^ [[Jefim Dinitz|Yefim Dinitz (1970). „Algorithm for solution of a problem of maximum flow in a network with power estimation” (PDF). Doklady Akademii nauk SSSR. 11: 1277–1280. Arhivirano iz originala (PDF) 22. 08. 2016. g. Pristupljeno 10. 04. 2017.]]
- ^ Ilan Kadar; Sivan Albagli (2009-11-27). [http://www.powershow.com/view/c6619-OThkZ/Dinitzs_algorithm_for_finding_a_maximum_flow_in_a_network_powerpoint_ppt_presentation „Dinitz's algorithm for finding a maximum flow in a network”].
- ^ Even, Shimon; Tarjan, R. Endre (1975). „Network Flow and Testing Graph Connectivity”. SIAM Journal on Computing. 4 (4): 507—518. ISSN 0097-5397. doi:10.1137/0204043.
- ^ Tarjan 1983. p. 102.