Диницов алгоритам
Диницов алгоритам је строго полиномијални алгоритам за израчунавање максималног протока кроз транспортну мрежу осмишљен 1970. године од стране израелског (претходно совјетског) изучивача компјутера Јефим Динитз[1][1] алгоритам се извршава у временском периоду О(В2Е) и сличан је Емонд-Карп Алгоритму који се извршава у времену О(ВЕ2) у томе да користи најкраће промењене путање. Увод концепта о графа са нивоима и блокирања тока омогућују Диницовом алгоритму да постигне своје извођење.
Историја
[уреди | уреди извор]Динитц алгоритам је 1970. године објавио бивши руски изучивач компјутера Јефим А. Динитц, који је данас члан Одсека за науку рачунарства нa Бен-Гурион Универзитету Негав (Израел), пре Едмондс-карп алгоритма који је објављен 1972. године али је раније откривен. Независно су показали да у Форд-фулкерсон алгоритму[2][2] ако је свака промењљива путања најкраћа, онда дужина променљивих путања не опада.
Дефиниција
[уреди | уреди извор]Нека је мрежа са и тежина и проток грана (у том редоследу).
- Преостала тежина је Сликање дефинисано као
- 1. ако
- 2. иначе
- 1. ако
- Преостали граф где:
- Промењљива путања је путања у преосталом графу .
- дефинишемо дист(в) да буде дужина накраће путање од с до в у графу . Онда граф са нивоима је граф где:
- Блокирајући ток је ток такав да граф са не садржи путању
Алгоритам
[уреди | уреди извор]Диницов алгоритам
- Улаз граф
- Излаз: ток максималне вредности
- иницијализујемо за свако
- Конструишемо уз помоћ од . Ако је стани и стави на излаз.
- Нађемо блокирајући ток у
- Ускладимо успомоћ и вратимо се на други корак
Анализа алгоритма
[уреди | уреди извор]Може бити показано да се број грана у сваком блокирајућем току повећава за барем 1 сваки пут тако да има највише блокирајућих токова у алгоритму, где је број чворова у графу. Граф са нивоима може бити конструисан претрагом у ширину у времену а блокирајући ток у сваком нивоу графа се може пронаћи у времену. Дакле Време извршавања овог алгоритма је .
Користећи структуру података звану динамичко дрве време потребно за налажење блокирајућег тока се може смањити на , па се време извршавања овог алгоритма може побољшати на .
Специјални случајеви
[уреди | уреди извор]У графу са јединичним тежинама, постоји много јача временска граница. Сваки блокирајући ток се може наћи за и може се показати да број фаза не прелази и . Тако да се алгоритам извршава у времену[3].
У графовима насталим током решавања проблема бипартитивног упаривања број фаза је ограничен са , одтле водећи временску границу . Резултујући алгоритам је познат као Хопцртфт-Карп алгоритам. Генералније ова граница држи било који граф -- граф у којем сваки чвор осим извора и понора има или једну улазну грану тежине један или једну излазну грану тежине један, а све остале тежине су произвољни цели бројеви.[4]
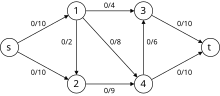
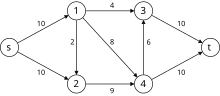
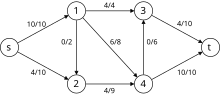
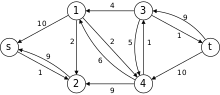
Пример
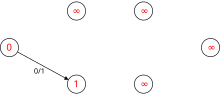
[уреди | уреди извор]Следеће је симулација динитц алгоритма. У гафу са нивоима чворови у црвеној боји су вредности . Путање плаве боје су блокирајући ток.
Види још
[уреди | уреди извор]Референце
[уреди | уреди извор]- ^ [[Јефим Динитз|Yefim Dinitz (1970). „Algorithm for solution of a problem of maximum flow in a network with power estimation” (PDF). Doklady Akademii nauk SSSR. 11: 1277–1280. Архивирано из оригинала (PDF) 22. 08. 2016. г. Приступљено 10. 04. 2017.]]
- ^ Ilan Kadar; Sivan Albagli (2009-11-27). [http://www.powershow.com/view/c6619-OThkZ/Dinitzs_algorithm_for_finding_a_maximum_flow_in_a_network_powerpoint_ppt_presentation „Dinitz's algorithm for finding a maximum flow in a network”].
- ^ Even, Shimon; Tarjan, R. Endre (1975). „Network Flow and Testing Graph Connectivity”. SIAM Journal on Computing. 4 (4): 507—518. ISSN 0097-5397. doi:10.1137/0204043.
- ^ Тарјан 1983. п. 102.