Piramida (geometrija)

Prave piramide sa regularnom osnovom
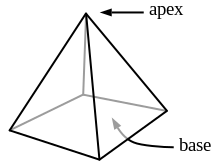Primer: kvadratna piramida
Strane	n trouglovi 1 n-sided poligon
Ivice	2n
Temena	n + 1
Šlaflijev simbol	( ) ∨ {n}
Konvejova notacija	Yn
Grupa simetrije	Cnv, [1,n], (*nn), reda 2n
Grupa rotacije	Cn, [1,n]+, (nn), reda n
Dualni poliedar	samodualan
Svojstva	konveksna

1-skelet piramide je dijagram točka

Osnovne dimenzije piramide

Piramida (od πυραμίς (pyramís)) poliedar je omeđen osnovom i stranicama koje se spajaju u jednoj tački - temenu, koje se nalazi na suprotnoj strani od osnove. Piramida može biti prava ili kosa. Prava piramida je ona kod koje se ortogonalna projekcija temena (vrha) na osnovu poklapa sa težištem osnove. Prava piramida je pravilna ako joj je osnova pravilan mnogougao. Površina piramide jednaka je zbiru površina osnove i stranica. Osnova može biti bilo koji mnogougao, dok su stranice zapravo trouglovi. Kod pravilne piramide ti trouglovi su jednakokraki i međusobno podudarni. Površina piramide se izračunava: $P=\ B+M$, gde je: B - površina osnove, M - površina omotača. Zapremina piramide se računa po formuli: $V={\frac {B*H}{3}}$, gde je: B - površina osnove, H - visina piramide

Među kosim piramidama, poput onih sa oštrim i tupim trouglovima, piramida se može nazvati oštrom ako je njen vrh iznad unutrašnjosti osnove i tupom ako joj je vrh iznad spoljašnjosti osnove. Pravougaona piramida ima vrh iznad ivice ili temena osnove. U tetraedru ovi kvalifikatori se menjaju na osnovu toga koje lice se smatra bazom.

Piramide su klasa prizmatoida. Piramide se mogu udvostručiti u bipiramide dodavanjem druge tačke pomeranja na drugoj strani osnovne ravni.

Prave piramide sa regularnom osnovom

Prava piramida sa regularnom osnovom ima stranice jednakokrakog trougla, sa simetrijom C_nv ili [1,n], i sa redom 2n. Njoj se može dati prošireni Šlafli simbol ( ) ∨ {n}, koji predstavlja tačku, ( ), spojenu (ortogonalno pomerenu) sa regularnim poligonom, {n}. Operacija spajanja stvara novu ivicu između svih parova temena dve spojene figure.

Trigonalna ili trouglasta piramida sa svim površinama jednakostraničnog trougla postaje regularni tetraedar, jedno od Platonovih čvrstih tela. Slučaj niže simetrije trouglaste piramide je C_3v, koja ima osnovu jednakostraničnog trougla i 3 identične stranice jednakokrakog trougla. Kvadratne i petougaone piramide takođe mogu biti sastavljene od pravilnih konveksnih mnogouglova, u kom slučaju su to Džonsonova tela.

Ako su sve ivice kvadratne piramide (ili bilo kog konveksnog poliedra) tangentne na sferu tako da je prosečan položaj tangencijalnih tačaka u centru sfere, tada se kaže da je piramida kanonska i čini polovinu pravilnog oktaedra.

Piramide sa šestouglom ili višom osnovom moraju biti sastavljene od jednakokrakih trouglova. Šestougaona piramida sa jednakostraničnim trouglovima bila bi potpuno ravna figura, a sedmougaona ili viša bi imala trouglove koji se uopšte ne bi sastajali.

Prava zvezdaste piramide

Pentagramska piramida

Prave piramide sa pravilnim zvezdastim poligonskim bazama nazivaju se zvezdaste piramide. Na primer, pentagramska piramida ima osnovu pentagrama i 10 trouglastih stranica koje se seku.

Prave piramide sa nepravilnom osnovom

Primer opšte prave piramide sa vrhom iznad težišta osnovnog poligona

Prava piramida se može nazvati kao ( )∨P, gde je ( ) tačka vrha, ∨ operator spajanja, i P je osnovni poligon.

Jednakostranični trougao pravog tetraedra može se napisati kao ( )∨[( )∨{ }] kao spoj tačke sa osnovom jednakokrakog trougla, kao [( )∨( )]∨{ } ili { }∨{ } kao spoj (ortogonalni pomaci) dva ortogonalna segmenta, digonalni disfenoid, koji sadrži 4 lica jednakokrakog trougla. On ima C_1v simetriju iz dve različite orijentacije baze i vrha, a C_2v u svojoj punoj simetriji.

Pravougaona prava piramida, napisana kao ( )∨[{ }×{ }], i rombična piramida, kao ( )∨[{ }+{ }], obe imaju simetriju C_2v.

Prave piramide

Pravougaona piramida	Rombična piramida

Zapremina

Vidi još: Kupa (geometrija)

Zapremina piramide (takođe bilo kojeg konusa) je $V={\tfrac {1}{3}}bh$, gde je b površina osnove, a h visina od osnove do vrha. Ovo funkcioniše za bilo koji poligon, pravilan ili nepravilan, i bilo koju lokaciju vrha, pod uslovom da se h meri kao okomito rastojanje od ravni koja sadrži osnovu. Godine 499, Arjabhata, matematičar-astronom iz klasičnog doba indijske matematike i indijske astronomije, koristio je ovu metodu u Arijabatiji (odeljak 2.6).

Formula se može formalno dokazati pomoću kalkulusa. Po sličnosti, linearne dimenzije poprečnog preseka paralelnog osnovici rastu linearno od vrha do osnove. Faktor skaliranja (faktor proporcionalnosti) je $1-{\tfrac {y}{h}}$, ili ${\tfrac {h-y}{h}}$, gde je h visina, a y okomito rastojanje od ravni osnove do poprečnog preseka. Pošto je površina bilo kog poprečnog preseka proporcionalna kvadratu faktora skaliranja oblika, površina poprečnog preseka na visini y je $b{\tfrac {(h-y)^{2}}{h^{2}}}$, ili pošto su b i h konstante, ${\tfrac {b}{h^{2}}}(h-y)^{2}$. Zapremina je data integralom

${\frac {b}{h^{2}}}\int _{0}^{h}(h-y)^{2}\,dy={\frac {-b}{3h^{2}}}(h-y)^{3}{\bigg |}_{0}^{h}={\tfrac {1}{3}}bh.$

Ista jednačina, $V={\tfrac {1}{3}}bh$, važi i za konuse sa bilo kojim baza. Ovo se može dokazati argumentom sličnim onom iznad; pogledajte zapreminu konusa.

Na primer, zapremina piramide čija je osnova n-strani pravilan mnogougao sa dužinom stranice s i čija je visina h je

$V={\frac {n}{12}}hs^{2}\cot {\frac {\pi }{n}}.$

Formula se takođe može izvesti tačno bez računa za piramide sa pravougaonim osnovama. Zamislite jediničnu kocku. Nacrtajte linije od centra kocke do svakog od 8 vrhova. Ovo deli kocku na 6 jednakih kvadratnih piramida osnovne površine 1 i visine 1/2. Svaka piramida jasno ima zapreminu od 1/6. Iz ovoga se zaključuje da je zapremina piramide = visina × površina osnove / 3.

Zatim se kocka može proširiti u tri pravca za nejednake količine tako da dobijene pravougaone čvrste ivice budu a, b i c, sa čvrstom zapreminom abc. Svaka od 6 piramida unutar nje je takođe proširena. Svaka piramida ima istu zapreminu abc/6. Pošto parovi piramida imaju visine a/2, b/2 i c/2, vidi se da je zapremina piramide = visina × površina osnove / 3 ponovo.

Kada su bočni trouglovi jednakostranični, formula za zapreminu je

$V={\frac {1}{12}}ns^{3}\cot \left({\frac {\pi }{n}}\right){\sqrt {1-{\frac {1}{4\sin ^{2}{\tfrac {\pi }{n}}}}}}.$

Ova formula važi samo za n = 2, 3, 4 i 5; a takođe pokriva slučaj n = 6, za koji je zapremina jednaka nuli (tj. visina piramide je nula).

Površina

Površina piramide je $SA=B+{\tfrac {1}{2}}PL$, gde je B osnovna površina, P je osnovni perimetar, a visina nagiba $L={\sqrt {h^{2}+r^{2}}}$, gde je h visina piramide, a r poluprečnik osnove.

Centroid

Centroid piramide nalazi se na segmentu prave koji povezuje vrh sa centroidom osnove. Za piramidu, težište je 1/4 udaljenosti od osnove do vrha.

n-dimenzionalne piramide

Dvodimenzionalna piramida je trougao, formiran od osnovne ivice povezane sa nekolinearnom tačkom koja se zove vrh.

4-dimenzionalna piramida se naziva poliedarska piramida, konstruisana od poliedra u 3-prostornoj hiperravni 4-prostora sa drugom tačkom izvan te hiperravne.

Piramide viših dimenzija su slično konstruisane.

Porodica simpleksa predstavlja piramide u bilo kojoj dimenziji, rastući od trougla, tetraedra, 5-ćelija, 5-simpleksa, itd. n-dimenzionalni simpleks ima minimum n+1 vrhova, sa svim parovima vrhova povezanih ivicama, sve trojke vrhova koji definišu lica, sve četvorke tačaka koje definišu tetraedarske ćelije, itd.

Poliedarska piramida

U 4-dimenzionalnoj geometriji, poliedarska piramida je 4-politop konstruisan od osnovne ćelije poliedra i tačke vrha. Bočni faseti su piramidalne ćelije, od kojih je svaka izgrađena od jedne strane osnovnog poliedra i vrha. Vrhovi i ivice poliedarskih piramida čine primere grafova vrhova, grafova formiranih dodavanjem jednog temena (vrha) na planarni graf (graf baze).

Regularni 5-ćelijski (ili 4-simpleks) je primer tetraedarske piramide. Uniformni poliedri sa poluprečnikom kruga manjim od 1 mogu se praviti poliedarske piramide sa pravilnim tetraedarskim stranicama. Poliedar sa v vrhovima, e ivicama i f površinama može biti osnova na poliedarskoj piramidi sa v+1 vrhovima, e+v ivicama, f+e površinama i 1+f ćelijama.

4D poliedarska piramida sa aksijalnom simetrijom može se vizualizovati u 3D pomoću Šlegelovog dijagrama — 3D projekcije koja postavlja vrh u centar osnovnog poliedra.

Jednakostranične uniformne piramide zasnovane na poliedru (Šlegelov dijagram)

Simetrija	[1,1,4]	[1,2,3]	[1,3,3]	[1,4,3]		[1,5,3]
Naziv	Kvadratno-piramidalna piramida	Trouglasto prizmatična piramida	Tetraedarska piramida	Kubna piramida	Oktaedarska piramida	Ikosaedarska piramida
Segmentohorni indeks	K4.4	K4.7	K4.1	K4.26.1	K4.3	K4.84
Visina	0,707107	0,645497	0,790569	0,500000	0,707107	0,309017
Slika (Osnova)
Osnova	Kvadratna piramida	Trouglasta prizma	Tetraedar	Kocka	Oktaedar	Ikosaedar

Svaki konveksni 4-politop se može podeliti na poliedarske piramide dodavanjem unutrašnje tačke i stvaranjem jedne piramide od svakog faseta do centralne tačke. Ovo može biti korisno za izračunavanje volumena.

4-dimenzionalna hiperzapremina poliedarske piramide je 1/4 zapremine osnovnog poliedra puta njegova visina okomito, u poređenju sa površinom trougla koja je 1/2 dužine osnove puta visina, i zapremina piramide da je 1/3 površine osnove puta visina.

3-dimenzionalna površinska zapremina poliedarske piramide je $SV=B+{\tfrac {1}{3}}AL$, gde je B osnovna zapremina, A je površina osnovne površine, a L visina nagiba (visina bočnih piramidalnih ćelija) $L={\sqrt {h^{2}+r^{2}}}$, gde je h visina, a r poluprečnik.

Vidi još

• Piramide (konstrukcije)
• Bipiramida
• Trigonalna piramida (hemija)

Literatura

• Tabak, John (2014). Geometry: the language of space and form. Infobase Publishing. str. xiv. ISBN 978-0-8160-4953-0. 
• Vincenzo De Risi (2015). Mathematizing Space: The Objects of Geometry from Antiquity to the Early Modern Age. Birkhäuser. str. 1—. ISBN 978-3-319-12102-4. 
• Walter A. Meyer (2006). Geometry and Its Applications. Elsevier. ISBN 978-0-08-047803-6. 
• J. Friberg, "Methods and traditions of Babylonian mathematics. Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations", Historia Mathematica, 8, 1981, pp. 277–318.
• Neugebauer, Otto (1969) [1957]. „Chap. IV Egyptian Mathematics and Astronomy”. The Exact Sciences in Antiquity (2 izd.). Dover Publications. str. 71—96. ISBN 978-0-486-22332-2. 
• Ossendrijver, Mathieu (29. 1. 2016). „Ancient Babylonian astronomers calculated Jupiter's position from the area under a time-velocity graph”. Science. 351 (6272): 482—484. Bibcode:2016Sci...351..482O. PMID 26823423. S2CID 206644971. doi:10.1126/science.aad8085. 
• Depuydt, Leo (1. 1. 1998). „Gnomons at Meroë and Early Trigonometry”. The Journal of Egyptian Archaeology. 84: 171—180. JSTOR 3822211. doi:10.2307/3822211. 
• Slayman, Andrew (27. 5. 1998). „Neolithic Skywatchers”. Archaeology Magazine Archive. Arhivirano iz originala 5. 6. 2011. g. Pristupljeno 17. 4. 2011. CS1 održavanje: Format datuma (veza)
• Eves, Howard (1990). An Introduction to the History of Mathematics. Saunders. ISBN 0-03-029558-0. , 1990, .
• Kurt Von Fritz (1945). „The Discovery of Incommensurability by Hippasus of Metapontum”. The Annals of Mathematics. 
• James R. Choike (1980). „The Pentagram and the Discovery of an Irrational Number”. The Two-Year College Mathematics Journal. 
• Eves, Howard (1990). An Introduction to the History of Mathematics. Saunders. ISBN 0-03-029558-0. .
• O'Connor, J.J.; Robertson, E.F. (februar 1996). „A history of calculus”. University of St Andrews. Arhivirano iz originala 15. 7. 2007. g. Pristupljeno 7. 8. 2007. CS1 održavanje: Format datuma (veza)
• Protter, Murray H.; Morrey, Jr., Charles B. (1970), College Calculus with Analytic Geometry (2nd izd.), Reading: Addison-Wesley, LCCN 76087042 

Spoljašnje veze

• Weisstein, Eric W. „Pyramid”. MathWorld.