Šestougao

Pravilni šestougao

U geometriji, šestougao ili heksagon je mnogougao sa šest temena i šest stranica.

Pravilni šestougao

Pravilni šestougao je šestougao kod koga su sve stranice jednake dužine i svi unutrašnji uglovi jednaki. Svaki unutrašnji ugao pravilnog šestougla ima po 120° (stepeni), a zbir svih unutrašnjih uglova bilo kog šestougla iznosi 720°. Kao što je moguće pokriti ravan jednakostraničnim trouglovima ili kvadratima, i pravilni šestougao ima tu osobinu, pa se može upotrebiti za konstruisanje teselacija. Pčelinje saće ima osnovne elemente u formi šestougla upravo zato što takav oblik omogućava efikasnu i ekonomičnu upotrebu prostora i materijala od koga je sagrađeno.

Ako primetimo da je pravilni šestougao sastavljen od 6 jednakostraničnih trouglova, njegova površina biće šest puta veća od površine jednakostraničnog trougla i, ako mu je osnovna stranica dužine $a\,\!$, biće data formulom $P=6\cdot {\frac {a^{2}{\sqrt {3}}}{4}}={\frac {3{\sqrt {3}}}{2}}a^{2}.$

Obim šestougla kome je stranica dužine $a\,\!$ biće jednak $6a\,\!$, dužina veće dijagonale je $2a\,\!$, a dužina kraće dijagonale je $a{\sqrt {3}}\,\!$.

Ne postoji Platonovo telo koje čine pravilni šestouglovi. Arhimedova tela koja su sastavljena i od šestouglova su zarubljeni tetraedar, zarubljeni oktaedar, zarubljeni ikosaedar (poznatiji kao fudbalska lopta), zarubljeni kuboktaedar i zarubljeni ikosidodeakedar.

Konstrukcija

Pravilni šestougao se može konstruisati uz pomoć lenjira i šestara. Sledeća animacija ilustruje korak po korak, konstrukciju pravilnog šestougla koju je dao Euklid, knjizi IV, svojih „Elemenata“.

Animirani prikaz konstrukcije šestougla pomoću šestara i lenjira

Parametri

Regularni šestougao

Maksimalni prečnik (koji odgovara dugoj dijagonali šestougla), D, je dvostruko veći od maksimalnog poluprečnika ili kružnog radijusa, R, koji je jednak dužini stranice, t. Minimalni prečnik ili prečnik upisane kružnice (razdvajanje paralelnih stranica, rastojanje od ravnog do ravnog, kratka dijagonala ili visina kada se oslanja na ravnu osnovu), d, je dvostruko veći od minimalnog poluprečnika ili inradijusa, r. Maksimum i minimum su povezani istim faktorom:

${\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t$     i, slično, $d={\frac {\sqrt {3}}{2}}D.$

Površina pravilnog šestougla

${\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\&\approx 2.598R^{2}\approx 3.464r^{2}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}$

Za bilo koji pravilan poligon, površina se takođe može izraziti u vidu apoteme a i perimetra p. Za pravilan šestougao oni su dati sa a = r, i p${}=6R=4r{\sqrt {3}}$, tako da je

${\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2}.\end{aligned}}$

Pravilan šestougao ispunjava razlomak ${\tfrac {3{\sqrt {3}}}{2\pi }}\approx 0.8270$ njegovog opisanog kruga.

Ako pravilni šestougao ima uzastopna temena A, B, C, D, E, F i ako je P bilo koja tačka na opisanoj kružnici između B i C, onda je PE + PF = PA + PB + PC + PD.

Iz odnosa radijusa opisanog i upisanog kruga sledi da je odnos visine i širine pravilnog šestougla 1:1,1547005; odnosno, šestougao sa dugačkom dijagonalom od 1,0000000 imaće rastojanje od 0,8660254 između paralelnih stranica.

Tačka u ravni

Za proizvoljnu tačku u ravni pravilnog šestougla sa kružnim radijusom $R$, čije su udaljenosti do centroida pravilnog šestougla i njegovih šest vrhova $L$ i $d_{i}$ respektivno, važe sledeće relacije

$d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2(R^{2}+L^{2}),$

$d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3(R^{2}+L^{2}),$

$d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3((R^{2}+L^{2})^{2}+2R^{2}L^{2}).$

Ako su $d_{i}$ rastojanja od temena pravilnog šestougla od bilo koje tačke na njegovoj opisanoj kružnici, onda je

$(\sum _{i=1}^{6}d_{i}^{2})^{2}=4\sum _{i=1}^{6}d_{i}^{4}.$

Simetrija

Primer šestouglova po simetriji
r12 regularan i4 d6 izotoksalan g6 usmeren p6 izogonalan d2 g2 generalni paralelogon p2 g3 a1

Šest linija refleksije pravilnog šestougla, sa Dih₆ ili r12 simetrijom, reda 12.

Diedralne simetrije se dele u zavisnosti od toga da li prolaze kroz vrhove (d za dijagonale) ili ivice (p za normale). Ciklične simetrije u srednjoj koloni su označene kao g za njihove centralne redove rotacije. Puna simetrija regularnog oblika je r12 i nijedna simetrija nije označena kao a1.

Pravilni šestougao ima Dih₆ simetriju, reda 12. Postoje tri diedarske podgrupe: Dih₃, Dih₂, i Dih₁ i četiri ciklične podgrupe: Z₆, Z₃, Z₂, i Z₁.

Ove simetrije izražavaju devet različitih simetrija pravilnog šestougla. Džon Konvej ih označava slovom i grupnim redosledom. r12 je puna simetrija, a a1 je odsustvo simetrija. p6, izogonalni šestougao konstruisan pomoću tri ogledala koji može da ima naizmenične duge i kratke ivice, i d6, izotoksalni šestougao konstruisan sa jednakim dužinama ivica, ali vrhovi naizmenično imaju dva različita unutrašnja ugla. Ove dve forme su dualne jedna drugoj i imaju upola manji red simetrije od pravilnog šestougla. Forme i4 su pravilni šestouglovi spljošteni ili rastegnuti duž jednog pravca simetrije. To se može videti kao izduženi romb, dok se d2 i p2 mogu videti kao horizontalno i vertikalno izduženi deltoidi. g2 šestouglovi, sa suprotnim stranicama koje su paralelne, nazivaju se i šestougaoni paralelogoni.

Svaka simetrija podgrupe dozvoljava jedan ili više stepeni slobode za nepravilne forme. Samo g6 podgrupa nema stepene slobode, ali se može posmatrati kao usmerene ivice.

Šestouglovi simetrije g2, i4, i r12, kao paralelogoni, mogu da oblikuju euklidsku ravan translacijom. Drugi šestougaoni oblici mogu popločati ravan sa različitim orijentacijama.

p6m (*632)	cmm (2*22)	p2 (2222)	p31m (3*3)	pmg (22*)		pg (××)
r12	i4	g2	d2	d2	p2	a1
Dih6	Dih2	Z2	Dih1			Z1

Disekcija

6-kubna projekcija	12 rombna disekcija

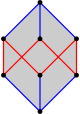
Kokseter navodi da se svaki zonogon (2m-gon čije su suprotne strane paralelne i jednake dužine) može secirati na m(m-1)/2 paralelograma. Ovo posebno važi za pravilne mnogouglove sa jednakim brojem strana, u kom slučaju su svi paralelogrami rombovi. Ova dekompozicija pravilnog šestougla je zasnovana na Petrijevoj poligonskoj projekciji kocke, sa 3 od 6 kvadratnih lica. Ostali paralelogoni i projektivni pravci kocke su raščlanjeni unutar pravougaonih kuboida.

Rastavljanje šestougla na tri romba i paralelograme
2D	Rombovi	Paralelogrami
	Regular {6}	Heksagonalni paralelogoni
3D	Kvadratna lica		Pravougaona lica
	Kocka		Pravougaoni kuboid

Povezani poligoni i pločice

Pravilan šestougao ima Šlaflijev simbol {6}. Pravilan šestougao je deo pravilnog heksagonalnog popločavanja, {6,3}, sa tri šestougaone strane oko svakog temena.

Pravilan šestougao se takođe može kreirati kao skraćeni jednakostranični trougao, sa Šlaflijevim simbolom t{3}. Gledano sa dve vrste (boje) ivica, ovaj oblik ima samo D₃ simetriju.

Skraćeni šestougao, t{6}, je dvanaestougao, {12}, koji naizmenično menja dve vrste (boje) ivica. Naizmenični šestougao, h{6}, je jednakostraničan trougao, {3}. Pravilan šestougao može biti zvezdast sa jednakostraničnim trouglovima na njegovim ivicama, stvarajući heksagram. Pravilan šestougao se može secirati na šest jednakostraničnih trouglova dodavanjem središnje tačke. Ovaj obrazac se ponavlja unutar regularnih trouglastih pločica.

Pravilan šestougao se može proširiti u regularan dvanaestougao dodavanjem naizmeničnih kvadrata i jednakostraničnih trouglovaa oko njega. Ovaj obrazac se ponavlja unutar rombitriheksagonalnih pločica.

Regularan {6}	Skraćen t{3} = {6}	Hiperskraćeni trouglovi			Stellated Zvezdasta figura 2{3}	Skraćeni t{6} = {12}	Naizmenični h{6} = {3}

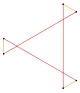
Ukršteni šestougao	Konkavni šestougao	Samopresecajući šestougao (zvezdasti poligon)	Prošireni Centralni {6} u {12}	Zakošeni šestougao, unutar kocke	Secirani {6}	Projekcija oktaedra	Kompletan graf

Gde se može videti šestougao

• U francuskom jeziku, termin l'hexagone (šestougao) se često koristi da označi Francusku, jer njen oblik podseća na šestougao.

• 
  Pogled iz vazduha na Fort Džeferson u nacionalnom parku Dry Tortugas
• 
  Pčelinje saće
• 
  Mikrofotografija snežne pahuljice

Vidi još

• Heksagonalni broj

Literatura

• Hahn, Theo, ur. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. International Tables for Crystallography. A (5th izd.). Berlin, New York: Springer-Verlag. ISBN 978-0-7923-6590-7. doi:10.1107/97809553602060000100. 
• Dana, James Dwight; Hurlbut, Cornelius Searle (1959). Dana's Manual of Mineralogy (17th izd.). New York: Chapman Hall. 
• Edward Prince (2004). Mathematical Techniques in Crystallography and Materials Science. Springer Science & Business Media. 
• „Medium-Resolution Space Group Diagrams and Tables”. img.chem.ucl.ac.uk. 
• Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics (1st izd.). str. 119. ISBN 0-03-083993-9. 
• Pough, Frederick H.; Peterson, Roger Tory (1998). A Field Guide to Rocks and Minerals. Houghton Mifflin Harcourt. str. 62. ISBN 0-395-91096-X. 
• Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th izd.). str. 78–89. ISBN 0-471-80580-7. 
• Graham, Dr. O.J. The Six-Pointed Star: Its Origin and Usage 4th ed. Toronto: The Free Press 777, 2001. ISBN 0-9689383-0-2
• Grünbaum, B. and G. C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
• Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70.

Spoljašnje veze

• Šestougao na Mathworld
• Definicija i osobine šestougla sa interaktivnom animacijom
• Weisstein, Eric W. „Hexagon”. MathWorld. 
• An Introduction to Hexagonal Geometry on Hexnet a website devoted to hexagon mathematics.
• Cassini Images Bizarre Hexagon on Saturn Arhivirano na sajtu Wayback Machine (27. septembar 2010)
• Saturn's Strange Hexagon Arhivirano na sajtu Wayback Machine (16. februar 2010)
• A hexagonal feature around Saturn's North Pole
• "Bizarre Hexagon Spotted on Saturn" – from Space.com (27 March 2007)