Претраживање успоном

У рачунарској науци, претраживање успоном је математичка оптимизациона техника која припада фамилији Локалне претраге. Ово је итеративан алгоритам који почиње са произвољним решењем за проблем, затим настоји да пронаће боље решење повећавајући један елемент решења. Ако промена повећањем елемента доведе до бољег решења, пронађено је боље решење. Ово понављамо све док више не буде било могуће да се нађе боље решење.

На пример, претраживање успоном се може применити на проблем трговачког путника. Лако је наћи почетно решење које посећује све градове, али неће бити оптимално решење. Алгоритам почиње са решењем и по мало га побољшавам као нпр. мењање редоследа по којем се два града посете. На крају ће се вероватно добити много краћи пут.

Претраживање успоном је добро за проналажење локалног оптимума (решење које се не може побољшати узимајући у обзир суседне конфигурације) али није засигурно гарантовано да ће се наћи најбоље могуће решење, глобални оптимум свих могућих решења решење кандидата). У конвексној оптимизацији проблема, Претраживање успоном је оптимално. Примери алгоритама који решавају конвексни проблем помоћу претраживања успоном су симплекс алгоритми за линеарно програмирање и бинарну претрагу.^[1]

Карактеристика коју само локални оптимум гарантује је побољшање помоћу рестартовања (понављана локална претрага), или више комплексније шеме засноване на итерацијама, као нпр итеративна локална претрага, на меморији, као оптимизација реактивне претраге и табу претрага, или меморијски-мање стохастичка мопдификација, као симулирано жарење.

Једноставност алгоритма га чини веома популарним и мећу првима за одабир из групе алгоритама оптимизације. Широко је коришћен у вештачкој интелигенцији, за достизање циља од почетног чвора. Избор следећег чвора и почетног чвора може бити различит дајући листу повезаних алгоритама. Иако сложенији алгоритми ако што су симулирано жарење или табу претрага могу дати боље резултате, у неким ситуацијама претраживање успоном ради савршено. Претраживање успоном често може изазвати боље резултате него остали алгоритми када је количина времена на располагању за извршење претраге ограничена, као што је у системима реалног времена. То је алгоритам за било које време: може да врати валидно решење чак и ако је прекинут пре завршетка.

Математички опис

Претраживање успоном настоји да увеличава (или смањује) циљ функцију $f(\mathbf {x} )$ , где $\mathbf {x}$ је континуирани вектор и/или дискретна вредност. У свакој итерацији , Претраживање успоном ће прилагодити један елемент у $\mathbf {x}$ и одредити да ли је промена побољшала вредност $f(\mathbf {x} )$ . (Приметити да је ово различити од алгоритма опадајућег градијента, који подешава вредности у $\mathbf {x}$ у свакој итерацији према градијенту Претраге успона) Са претрагом успона, свака промена која побољшава $f(\mathbf {x} )$ је прихваћена, и процес се наставља све док више не буде било промена за побољшање вредности $f(\mathbf {x} )$ . Онда $\mathbf {x}$ се каже да је "локални оптимум".

У дискретним векторским просторима, свака могућа вредност за $\mathbf {x}$ може се приказати као чвор у графу. Претраживање успоном ће пратити граф од чвора до чвора, увек локалну повећавати (или смањивати) вредност $f(\mathbf {x} )$ , све док локални максимум (или локални минимум) $x_{m}$ је достигнут.

Варијанте

У једноставном претраживању успоном, први ближи чвор се узима, док у сложенијем претраживању успоном сви наследници се пореде и онај најближи решењу се узима. Оба облика неће успети ако нема чвора који је у близини, што се може десити ако постоје локални максимуми у простору претраге такви да нису решења. Сложенији алгоритам је сличан алгоритму претраге по најбољим особинама, који покушава све могуће додатке тренутне путање уместо само једне путање.

Стохастичко претраживање успоном не испитује све суседе пре него што одлучи како ће се кретати. Радије, случајним избором бира чвор, и одлучује (на основу количине побољшања тог суседа) да ли да се креће ка том суседу или да испитује други.

Координатно спуштање ради линијску претрагу дуж праваца једне координате на тренутној тачки у свакој итерацији. Неке верзије координатног спуштања насумично узимају различите координате праваца у свакој итерацији.

Случајно-рестартовање претраживања успоном је мета алгоритам изгражен на врху алгоритма Претраге успоном. Итеративно ради претрагу успоном, сваки пут са случајно изабраним почетним условом $x_{0}$ . Најбоље $x_{m}$ се чува: ако је нови резултат претраге успоном болље $x_{m}$ него смештено стање, онда оно мења смештено стање.

Случајно-рестартовање претраживањем успоном је изненаћујуће ефективан алгоритам у многим случајевима. Испоставило се да је често боље потрошити време процесора претражујући простор, него пажљиво оптимизујући почетни услов.

Проблеми

Локални максимум

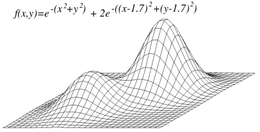
Претраживање успоном неће нужно наћи глобални максимум, али може конвергирати ка локалном максимуму. Овај проблем се не појављује ако је хеуристика конвексна. Међутим, пошто много функција нису конвексне претраживање успоном може често да не успе у проналаску глобалног максимума. Други алгоритми локалне претраге покушавају да превазиђу овај проблем као стохастичка претрага успоном, случајна шетња и симулирано жарење.

Упркос много локалних максимума у овом графу, глобални максимум се може и даље наћи симулираним жарењем. Нажалост, примењивост симулираног жарења је специфичан проблем зато што се ослања на проналажење *срећни скокови* који побољшавају позицију. У проблемима који укључују више димензија, цена проналаска таквог скока може бити експоненцијална у зависности са димензијом. Сходно томе, постоје многи проблеми за које претраживање успоном ће ефикасно наћи добро решење док симулирано жарење ће наизглед тражити заувек без икаквог напредка. Овај приказ показује један екстреман случај који укључује само једну димензију.

Гребени и долине

Гребени су изазовни проблеми за претраживање успоном који се оптимизује у трајним простоимау. Пошто претрага успоном подешава само један елемент у вектору, сваки корак ће се померати у правцу икс кординате. Ако циљана функција прави узак гребен који се повећава у правцу не-икс осе (или ако је циљ минимизација, уска долина која опада у не-икс правцу), онда претрага успоном може само повећати гребен (или смањити долину) шеврдањем. Ако су стране гребена (или долине) веома стрме, онда претрага може бити натерана да прави веома мале кораке попут шеврдања ка бољој позицији. Тако, може одузети много времена аза повећање гребена (или смањење долине).

Помоћу контраста , алгоритам опадајућег градијента се може кретати у било ком правцу за који гребен или долина расту или опадају. Отуда, алгоритам опадајућег градијента је генерално пожељан током претраге успона када је циљана функција диференцијабилна. Претраживање успоном, има предност да циљана функције не мора да буде диференцијабилна, па се зато ова претрага може користити када је циљана функција комплексна.

Висораван

Другги проблем који се некад појављује са претрагом успона је висораван. Висораван постоји када је претрага простора равна, или довољно равна да враћена вредност циљане функције буде разлицита од вредности враћене из блиског региона због прецизности коју користи машина да прикаже њену вредност. У таквим случајевима , претрага успоном не може одредити у ком правцу треба да иде, и може отићи у правац који никад не води до напретка.

Псеудокод


Diskretno prostorni algoritam pretrazivanja usponom
   trenutniCvor = pocetniCvor;
   loop do
      L = SUSEDI(trenutniCvor);
      sledecaProc = -BESKONACNO;
      sledeciCvor = NULL;
      for all x in L 
         if (PROCENA(x) > sledecaProc)
              sledeciCvor = x;
              sledecaProc= PROCENA(x);
      if sledecaProc <= PROCENA(trenutniCvor)
         //Vraca tenutni cvor posto ne postoji bolji komsija
         return trenutniCvor;
      trenutniCvor = sledeciCvor;

Kontinuirano prostorni algoritam pretrazivanja usponom
   trenutnaTacka = pocetnaTacka;    // нула степени вектор је заједнички
   velKoraka = inicijalizujVelKoraka;    // вектор свих 1 је заједнички
   ubrzanje = nekoUbrzanje; // вредност 1.2 је заједничка
   kandidat[0] = -ubrzanje;
   kandidat[1] = -1 / ubrzanje;
   kandidat[2] = 0;
   kandidat[3] = 1 / ubrzanje;
   kandidat[4] = ubrzanje;
   loop do
      pre = PROCENA(trenutnaTacka );
      for each element i in trenutnaTacka do
         najbolje = -1;
         najboljiRez = -BESKONACNO;
         for j from 0 to 4         // probaj svaku od 5 kandidatovih lokacija
            trenutnaTacka [i] = trenutnaTacka [i] + velKoraka[i] * kandidat[j];
            temp = PROCENA(trenutnaTacka );
            trenutnaTacka [i] = trenutnaTacka [i] - velKoraka[i] * kandidat[j];
            if(temp > najboljiRez )
                 najboljiRez = temp;
                 najbolje = j;
         if kandidat[najbolje ] is not 0
            trenutnaTacka [i] = trenutnaTacka [i] + velKoraka[i] * kandidat[najbolje];
            stepSize[i] = velKoraka[i] * kandidat[najbolje]; // ubrzaj
      if (PROCENA(trenutnaTacka ) - pre) < epsilon 
         return trenutnaTacka ;

Контраст Генетски алгоритам; Случајна оптимизација.

Види још

Референце

^ Skiena 2010, стр. 253.

Литература

Skiena, Steven (2010). The Algorithm Design Manual (2nd изд.). Springer Science+Business Media. ISBN 978-1-84996-720-4.

Спољашње везе

Hill Climbing visualization Архивирано на сајту Wayback Machine (30. август 2009) Визуелизација претраге успоном (похлепан алгоритам) решење за N-Queens пузле од Yuval Baror.

[FOOTNOTESkiena2010253-1] Skiena 2010, стр. 253.

[1]