Pretraživanje usponom

U računarskoj nauci, pretraživanje usponom je matematička optimizaciona tehnika koja pripada familiji Lokalne pretrage. Ovo je iterativan algoritam koji počinje sa proizvoljnim rešenjem za problem, zatim nastoji da pronaće bolje rešenje povećavajući jedan element rešenja. Ako promena povećanjem elementa dovede do boljeg rešenja, pronađeno je bolje rešenje. Ovo ponavljamo sve dok više ne bude bilo moguće da se nađe bolje rešenje.

Na primer, pretraživanje usponom se može primeniti na problem trgovačkog putnika. Lako je naći početno rešenje koje posećuje sve gradove, ali neće biti optimalno rešenje. Algoritam počinje sa rešenjem i po malo ga poboljšavam kao npr. menjanje redosleda po kojem se dva grada posete. Na kraju će se verovatno dobiti mnogo kraći put.

Pretraživanje usponom je dobro za pronalaženje lokalnog optimuma (rešenje koje se ne može poboljšati uzimajući u obzir susedne konfiguracije) ali nije zasigurno garantovano da će se naći najbolje moguće rešenje, globalni optimum svih mogućih rešenja rešenje kandidata). U konveksnoj optimizaciji problema, Pretraživanje usponom je optimalno. Primeri algoritama koji rešavaju konveksni problem pomoću pretraživanja usponom su simpleks algoritmi za linearno programiranje i binarnu pretragu.^[1]

Karakteristika koju samo lokalni optimum garantuje je poboljšanje pomoću restartovanja (ponavljana lokalna pretraga), ili više kompleksnije šeme zasnovane na iteracijama, kao npr iterativna lokalna pretraga, na memoriji, kao optimizacija reaktivne pretrage i tabu pretraga, ili memorijski-manje stohastička mopdifikacija, kao simulirano žarenje.

Jednostavnost algoritma ga čini veoma popularnim i meću prvima za odabir iz grupe algoritama optimizacije. Široko je korišćen u veštačkoj inteligenciji, za dostizanje cilja od početnog čvora. Izbor sledećeg čvora i početnog čvora može biti različit dajući listu povezanih algoritama. Iako složeniji algoritmi ako što su simulirano žarenje ili tabu pretraga mogu dati bolje rezultate, u nekim situacijama pretraživanje usponom radi savršeno. Pretraživanje usponom često može izazvati bolje rezultate nego ostali algoritmi kada je količina vremena na raspolaganju za izvršenje pretrage ograničena, kao što je u sistemima realnog vremena. To je algoritam za bilo koje vreme: može da vrati validno rešenje čak i ako je prekinut pre završetka.

Matematički opis

Pretraživanje usponom nastoji da uveličava (ili smanjuje) cilj funkciju $f(\mathbf {x} )$ , gde $\mathbf {x}$ je kontinuirani vektor i/ili diskretna vrednost. U svakoj iteraciji , Pretraživanje usponom će prilagoditi jedan element u $\mathbf {x}$ i odrediti da li je promena poboljšala vrednost $f(\mathbf {x} )$ . (Primetiti da je ovo različiti od algoritma opadajućeg gradijenta, koji podešava vrednosti u $\mathbf {x}$ u svakoj iteraciji prema gradijentu Pretrage uspona) Sa pretragom uspona, svaka promena koja poboljšava $f(\mathbf {x} )$ je prihvaćena, i proces se nastavlja sve dok više ne bude bilo promena za poboljšanje vrednosti $f(\mathbf {x} )$ . Onda $\mathbf {x}$ se kaže da je "lokalni optimum".

U diskretnim vektorskim prostorima, svaka moguća vrednost za $\mathbf {x}$ može se prikazati kao čvor u grafu. Pretraživanje usponom će pratiti graf od čvora do čvora, uvek lokalnu povećavati (ili smanjivati) vrednost $f(\mathbf {x} )$ , sve dok lokalni maksimum (ili lokalni minimum) $x_{m}$ je dostignut.

Varijante

U jednostavnom pretraživanju usponom, prvi bliži čvor se uzima, dok u složenijem pretraživanju usponom svi naslednici se porede i onaj najbliži rešenju se uzima. Oba oblika neće uspeti ako nema čvora koji je u blizini, što se može desiti ako postoje lokalni maksimumi u prostoru pretrage takvi da nisu rešenja. Složeniji algoritam je sličan algoritmu pretrage po najboljim osobinama, koji pokušava sve moguće dodatke trenutne putanje umesto samo jedne putanje.

Stohastičko pretraživanje usponom ne ispituje sve susede pre nego što odluči kako će se kretati. Radije, slučajnim izborom bira čvor, i odlučuje (na osnovu količine poboljšanja tog suseda) da li da se kreće ka tom susedu ili da ispituje drugi.

Koordinatno spuštanje radi linijsku pretragu duž pravaca jedne koordinate na trenutnoj tački u svakoj iteraciji. Neke verzije koordinatnog spuštanja nasumično uzimaju različite koordinate pravaca u svakoj iteraciji.

Slučajno-restartovanje pretraživanja usponom je meta algoritam izgražen na vrhu algoritma Pretrage usponom. Iterativno radi pretragu usponom, svaki put sa slučajno izabranim početnim uslovom $x_{0}$ . Najbolje $x_{m}$ se čuva: ako je novi rezultat pretrage usponom bollje $x_{m}$ nego smešteno stanje, onda ono menja smešteno stanje.

Slučajno-restartovanje pretraživanjem usponom je iznenaćujuće efektivan algoritam u mnogim slučajevima. Ispostavilo se da je često bolje potrošiti vreme procesora pretražujući prostor, nego pažljivo optimizujući početni uslov.

Problemi

Lokalni maksimum

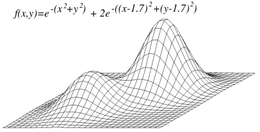
Pretraživanje usponom neće nužno naći globalni maksimum, ali može konvergirati ka lokalnom maksimumu. Ovaj problem se ne pojavljuje ako je heuristika konveksna. Međutim, pošto mnogo funkcija nisu konveksne pretraživanje usponom može često da ne uspe u pronalasku globalnog maksimuma. Drugi algoritmi lokalne pretrage pokušavaju da prevaziđu ovaj problem kao stohastička pretraga usponom, slučajna šetnja i simulirano žarenje.

Uprkos mnogo lokalnih maksimuma u ovom grafu, globalni maksimum se može i dalje naći simuliranim žarenjem. Nažalost, primenjivost simuliranog žarenja je specifičan problem zato što se oslanja na pronalaženje *srećni skokovi* koji poboljšavaju poziciju. U problemima koji uključuju više dimenzija, cena pronalaska takvog skoka može biti eksponencijalna u zavisnosti sa dimenzijom. Shodno tome, postoje mnogi problemi za koje pretraživanje usponom će efikasno naći dobro rešenje dok simulirano žarenje će naizgled tražiti zauvek bez ikakvog napredka. Ovaj prikaz pokazuje jedan ekstreman slučaj koji uključuje samo jednu dimenziju.

Grebeni i doline

Grebeni su izazovni problemi za pretraživanje usponom koji se optimizuje u trajnim prostoimau. Pošto pretraga usponom podešava samo jedan element u vektoru, svaki korak će se pomerati u pravcu iks kordinate. Ako ciljana funkcija pravi uzak greben koji se povećava u pravcu ne-iks ose (ili ako je cilj minimizacija, uska dolina koja opada u ne-iks pravcu), onda pretraga usponom može samo povećati greben (ili smanjiti dolinu) ševrdanjem. Ako su strane grebena (ili doline) veoma strme, onda pretraga može biti naterana da pravi veoma male korake poput ševrdanja ka boljoj poziciji. Tako, može oduzeti mnogo vremena aza povećanje grebena (ili smanjenje doline).

Pomoću kontrasta , algoritam opadajućeg gradijenta se može kretati u bilo kom pravcu za koji greben ili dolina rastu ili opadaju. Otuda, algoritam opadajućeg gradijenta je generalno poželjan tokom pretrage uspona kada je ciljana funkcija diferencijabilna. Pretraživanje usponom, ima prednost da ciljana funkcije ne mora da bude diferencijabilna, pa se zato ova pretraga može koristiti kada je ciljana funkcija kompleksna.

Visoravan

Druggi problem koji se nekad pojavljuje sa pretragom uspona je visoravan. Visoravan postoji kada je pretraga prostora ravna, ili dovoljno ravna da vraćena vrednost ciljane funkcije bude razlicita od vrednosti vraćene iz bliskog regiona zbog preciznosti koju koristi mašina da prikaže njenu vrednost. U takvim slučajevima , pretraga usponom ne može odrediti u kom pravcu treba da ide, i može otići u pravac koji nikad ne vodi do napretka.

Pseudokod


Diskretno prostorni algoritam pretrazivanja usponom
   trenutniCvor = pocetniCvor;
   loop do
      L = SUSEDI(trenutniCvor);
      sledecaProc = -BESKONACNO;
      sledeciCvor = NULL;
      for all x in L 
         if (PROCENA(x) > sledecaProc)
              sledeciCvor = x;
              sledecaProc= PROCENA(x);
      if sledecaProc <= PROCENA(trenutniCvor)
         //Vraca tenutni cvor posto ne postoji bolji komsija
         return trenutniCvor;
      trenutniCvor = sledeciCvor;

Kontinuirano prostorni algoritam pretrazivanja usponom
   trenutnaTacka = pocetnaTacka;    // нула степени вектор је заједнички
   velKoraka = inicijalizujVelKoraka;    // вектор свих 1 је заједнички
   ubrzanje = nekoUbrzanje; // вредност 1.2 је заједничка
   kandidat[0] = -ubrzanje;
   kandidat[1] = -1 / ubrzanje;
   kandidat[2] = 0;
   kandidat[3] = 1 / ubrzanje;
   kandidat[4] = ubrzanje;
   loop do
      pre = PROCENA(trenutnaTacka );
      for each element i in trenutnaTacka do
         najbolje = -1;
         najboljiRez = -BESKONACNO;
         for j from 0 to 4         // probaj svaku od 5 kandidatovih lokacija
            trenutnaTacka [i] = trenutnaTacka [i] + velKoraka[i] * kandidat[j];
            temp = PROCENA(trenutnaTacka );
            trenutnaTacka [i] = trenutnaTacka [i] - velKoraka[i] * kandidat[j];
            if(temp > najboljiRez )
                 najboljiRez = temp;
                 najbolje = j;
         if kandidat[najbolje ] is not 0
            trenutnaTacka [i] = trenutnaTacka [i] + velKoraka[i] * kandidat[najbolje];
            stepSize[i] = velKoraka[i] * kandidat[najbolje]; // ubrzaj
      if (PROCENA(trenutnaTacka ) - pre) < epsilon 
         return trenutnaTacka ;

Kontrast Genetski algoritam; Slučajna optimizacija.

Vidi još

Reference

^ Skiena 2010, str. 253.

Literatura

Skiena, Steven (2010). The Algorithm Design Manual (2nd izd.). Springer Science+Business Media. ISBN 978-1-84996-720-4.

Spoljašnje veze

Hill Climbing visualization Arhivirano na sajtu Wayback Machine (30. avgust 2009) Vizuelizacija pretrage usponom (pohlepan algoritam) rešenje za N-Queens puzle od Yuval Baror.

[FOOTNOTESkiena2010253-1] Skiena 2010, str. 253.

[1]