1 + 1 + 1 + 1 + ...

Низ 1 + 1 + 1 + 1 + ⋯

Након изравнања

Асимптотско понашање изравнања. У-пресек линије је -1/2.

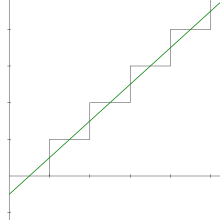
У математици,  1 + 1 + 1 + 1 + · · ·, написано и као $\sum _{n=1}^{\infty }n^{0}$, $\sum _{n=1}^{\infty }1^{n}$, или једноставно $\sum _{n=1}^{\infty }1$, је дивергентни ред, што значи да низ парцијалних сума не конвергира до границе у реалним бројевима. Низ 1ⁿ може се посматрати као геометријски низ са заједничким односом 1. За разлику од других геометријских низова са рационалним односом (осим -1), не конвергира у реалне бројеве, ни у р–адске бројеве за неко p. У контексту проширене линије реалног броја

$\sum _{n=1}^{\infty }1=+\infty \,,$

јер се њен низ парцијалних сума повећава монотоно без граница.

Где се збир n⁰ јавља у физичким апликација, понекад може да се тумачи од зета функције регулисања. То је вредност на s = 0 Риманове зета функције.

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,,$

Две горенаведене формуле не важе за нулу, међутим, како једна мора да користи аналитички наставак Риманове зета функције,

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!,$

Користећи овај добија се (с обзиром да је $\Gamma (1)=1$),

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right)=-{\frac {1}{2}}\!$

где експанзија снаге низа за ζ(s) око s = 1 прати јер ζ(s) има једноставан пол остатака једног тамо. У том смислу 1 + 1 + 1 + 1 + · · · = ζ(0) = −¹⁄₂.

Емилио Елизалде представља анегдоту о ставовима према редовима:

За кратак период мањи од једне године, два угледна физичара, А. Славнов и Ф. Јнудараин, су дала семинаре у Барселони, о различитим темама. Било је невероватно да се, у обе презентације, у једном тренутку говорник обратио следећим речима: "Као што сви знају, 1 + 1 + 1 + · · · = −¹⁄₂'. Имплицира можда: Ако не знате ово, нема сврхе да наставите да слушате.

Види још

• 1 − 1 + 2 − 6 + 24 − 120 + · · ·
• Хармонијски редови