Nauka o čvrstoći

Silnice unutrašnjih sila su gušće u blizini rupe (uobičajeni raspored naprezanja).

Greda je izdužena vodoravna ili kosa nosiva građevna konstrukcija za prenošenje vertikalnih opterećenja na ležaje, oslonjena na svojim krajevima (na jednoj strani pomično, na drugoj nepomično). Prema broju ležaja razlikuju se greda s jednim ležajem (konzolna), s dva ležaja (prosto oslonjena, s prepustima), s više ležaja (kontinuirana).

Opruga za koju vredi Hukov zakon: sila F je srazmerna (proporcionalna) rastezanju opruge x.

Zatezno ispitivanje na kidalici za nestandardni ispitni uzorak.

Naprezanje $\sigma =F/A$ uglavnom je prosečno naprezanje u preseku. Naprezanje se često ne raspoređuje jednako u preseku (m–m), posebno u blizini mesta gde deluje spoljašnja sila u hvatištu (n–n'').

Dijagram naprezanja (σ - zateznog naprezanja i ε - linijske zatezne deformacije) za tipični neželjezni materijal:
1: Stvarna granica elastičnosti
2: Granica proporcionalnosti
3: Granica elastičnosti
4: Granica razvlačenja ili σ_0,2 (naprezanje pri kojem nastaje trajno produženje od 0,2% prvobitne dužine šipke ili štapa)

Klizačica kod okretanja smanjuje svoj moment inercije skupljajući ruke uz telo kako bi se brže okretala.

Traktor sa spoljašnjim zamašnjakom (s velikim momentom inercije) koji služi da ujednačuje okretanje motora (bez trzaja).

Materijal može biti opterećen a) pritisno, b) zatezno, c) smično.

Spoj za toplotno istezanje na mostu.

Uvijanje ili torzija šipke (štapa) kvadratnog preseka.

Moment savijanja uzrokuje normalna naprezanja σ koja se zamišljaju razdeljenima po preseku srazmerno udaljenosti od neutralne osi.

Slika opterećenja grede na 2 oslonca, delovanje sila na gredu, delovanje momenata savijanja na gredu i progib grede kada normalna sila deluje u sredini grede.

Kod smicanja sila se primjenjuje na vrh pravougaonika dok je dno pravougaonika u mestu. Nastalo smično naprezanje, $\tau \,$, izobličuje pravougaonik u paralelogram, tako da je opterećen samo vrh paralelograma.

Prikaz 4 Ojlerova modela izvijanja kada nastaje gubitak stabilnosti štapa ili nekog drugog vitkog elementa konstrukcije (na primer stuba) osno opterećenoga prekomerno velikom pritisnom silom.

Nauka o čvrstoći je grana mehanike koja proučava čvrstoću, krutost i stabilnost konstrukcija i mašina, te jednostavnih konstrukcijskih celina. Čvrstoća konstrukcije je sposobnost prenošenja sila i opterećenja bez loma materijala, trajnih plastičnih deformacija ili oštećenja (pukotina). Krutost konstrukcije je otpornost konstrukcije prema deformiranju. Elastična stabilnost konstrukcije je sposobnost konstrukcije da zadrži početan ravnotežni oblik. Gubitak elastične stabilnosti naziva se izvijanje.

Osim naziva nauka o čvrstoći upotrebljava se i naziv otpornost materijala. Oba su naziva tradicionalna i ne odgovaraju u potpunosti. Ne radi se o otpornosti (čvrstoći) materijala, nego o čvrstoći delova konstrukcija. Osim čvrstoće proučava se još krutost i stabilnost, pa ni naziv nauka o čvrstoći nije potpuno prikladan, iako je bolji od naziva otpornost materijala. Bolji naziv bio bi mehanika deformabilnih čvrstih tela, slično nazivu mehanika krutih tela ili mehanika fluida. Nauka o čvrstoći je u prvom redu tehnička (inženjerska) disciplina kojoj je svrha da što jednostavnijim metodama na zadovoljavajući, približan način reši probleme iz tehničke prakse. Ponekad se susreće i naziv elastostatika, koja proučava statičke probleme elastičnih tela. Ni taj naziv nije dobra zamena za naziv nauka o čvrstoći, jer ona proučava i neelastična tela i dinamičke probleme, pa se čini opravdanim zadržati naziv nauka o čvrstoći.

Istorija

Već na početku razvoja civilizacije, kad su se počele graditi veće zgrade, hramovi, mostovi, brodovi, jednostavne mašine i naprave, bilo je potrebno da se sakupe podaci o svojstvima pojedinih konstrukcijskih materijala i oblika tela. Bez sumnje su postojala iskustvena pravila o određivanju mera pojedinih delova konstrukcija, jer bi bez njih bilo nemoguće izgraditi veličanstvene građevine i spomenike izgrađene još u starom veku. Posebno su se svojim građevinarstvom isticali graditelji Rimskog carstva. Poznate su njihove palate, hramovi, arene, bazilike, akvedukti, te katapulti i druge ratne i radne mašine. Nešto o metodama njihova graditeljstva poznato je iz knjige De architectura libri decem od Marka Poliona Vitruvija. Najveći deo znanja koji su sakupili stari Grci i Rimljani i drugi narodi izgubljen je u toku ranoga srednjeg veka.

Prve značajne eksperimente o ponašanju i čvrstoći materijala obavio je Leonardo da Vinči na prelazu iz 15. u 16. vek. On je ispitivao čvrstoću žice, greda i stubova. Došao je do ispravnog zaključka da je čvrstoća grede na dva oslonca srazmerna (proporcionalna) širini i obrnuto srazmerna rasponu. Nije zabeleženo da li je ispitivao uticaj visine grede. Galileo Galilej je prvi pokušao da analitički odredi čvrstoću pojedinih delova konstrukcija. Utvrdio je da čvrstoća geometrijski sličnih tela opada s porastom dimenzija. Poznata su njegova razmatranja o savijanju štapa. On je pogrešno pretpostavio da su sile (naprezanje) pri savijanju jednoliko raspodeljene po visini preseka grede i da se greda pri lomu okreće oko najniže tačke oslonca. Uz tu pretpostavku ravnoteža momenata unutrašnjih i spoljašnjih sila oko ukleštenog kraja pravougaone (dužine l, širine b i visine h) konzole daje:

$\sigma =2\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

Tačno rešenje glasi:

$\sigma =6\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

Galilejevo rešenje razlikuje se samo za konstantu od tačnog rešenja. Galileo je objavio u delu Discorsi e dimostrazioni matematische intorno a due nuove scienze attenenti alla meccanica & i movimenti locali (Lejden, 1638).

Problem savijanja grede obrađivao je i Edm Mariot. On je u radu objavljenom 1690. zadržao pretpostavku da neutralna linija prolazi kroz donji brid preseka, ali je uveo pretpostavku da naprezanja linearno rastu došao je do rešenja:

$\sigma =3\cdot {\frac {F\cdot l}{b\cdot h^{2}}}$

To je rešenje bliže tačnom od Galilejevog. Antvan Parent (16. septembra 1666. – 26. septembra 1716) je takođe razmatrao savijanje grede. On je 1713. objavio dva rada. U prvom je pokazao da Mariotovo rešenje može vrediti samo za pravougaoni presek i izveo je izraz za kružni presek. U drugom radu je pošao od pretpostavke da neutralna osa prolazi kroz sredinu preseka i došao do ispravnog rešenja. Njegov je rad, međutim, ostao nezapažen, pa su se mnogi inženjeri i dalje služili Mariotovim rešenjem. Tačno rešenje problema savijanja grede izveo je 1773. Šarl-Ogisten de Kulon ne poznavajući Parentovo rešenje. On je 1784. rešio problem uvijanja okruglog štapa i uveo pojam modula smicanja.

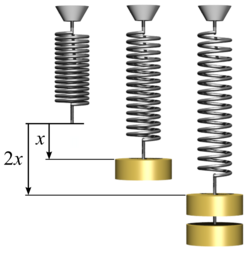
Zakon linearne zavisnosti opterećenja i pomaka, odnosno naprezanja i deformacije postavio je 1660. Robert Huk na temelju eksperimenta s oprugama. Međutim, taj zakon, poznat kao Hukov zakon, objavljen je tek 1678. u knjizi De potentia restitutiva, sa objašnjenjem kakva sila, takvo produljenje. Tomas Jang je 1807. matematički izveo Hukeov zakon za jednoosno rastezanje i uveo pojam modula elastičnosti, koji se po njemu naziva i Jangov modul elastičnosti. Taj je zakon 1828. dopunio Simeon Deni Poason i uveo pojam koeficijenta poprečne konstrukcije pri rastezanju, koji se po njemu naziva Poasonov koeficijent ili Poasonov odnos.

Znatno su pridoneli razvoju teorije elastičnosti i analitičkim metodama o nauci o čvrstoći švajcarski matematičari, braća Jakob i Johan Bernuli. Oni su razmatrali deformacije grede pri savijanju. Jakob Bernuli je uveo pretpostavku da pri savijanju poprečni preseci ostaju ravni. On je 1694. utvrdio da je zakrivljenost elastične linije proporcionalna momentu savijanja. Danijel Bernuli, Johanov sin, prvi je izveo diferencijalnu jednakost poprečnih vibracija štapa. Leonard Ojler, učenik Danijela Bernulija, takođe je proučavao elastične linije. On je 1744. izveo izraz za kritičnu silu izvijanja vitkog štapa. Ogisten Luj Koši je 1822. u radu koji je predložio Francuskoj akademiji nauka, po prvi put odredio prostorno stanje naprezanja i izveo jednakosti ravnoteže diferencijalnog elementa. Prvi rad iz teorije ploča objavio je Klod Luj Navje 1820. On je takođe prvi dao opšti pristup rešavanju statički neodređenih zadataka. Teoriju savijanja ploča razrađivali su dalje Simeon Deni Poason, Gustaf Kirhof i drugi. D. J. Žuravski je izveo 1844. izraz za pomična naprezanja pri savijanju grede. Emil Vinkler je 1858. rešio problem savijanja debelog zakrivljenog štapa metodama nauke o čvrstoći. Tačno rešenje tog problema dao je 1881. M. Golovin. Uvijanja nekih neokruglih preseka rešio je 1852. Ademar Žan-Klod Bare de Sen-Venan. Godine 1857. Emil Klapejron izveo je jednakost tri momenata (Klapejronova jednakost). Džejms Klerk Maksvel je 1870. izveo teoremu o recipročnosti uplivnih koeficijenata (Maksvelova teorema), a Karlo Alberto Kaztiljijano je 1873. izveo svoju prvu teoremu. Kristijan Oto Mor je objavio rad o kružnicama naprezanja 1895.

Naprezanje

Glavni članak: Naprezanje

Naprezanje je unutarnja sila raspodeljena po jedinici površine nekog čvrstog tela koja se javlja kao reakcija na delovanje spoljašnjih sila ili promene temperature tela, s jedinicom paskal (Pa = N/m²). Veličina naprezanja u nekoj tački tela zavisi od orijentacije preseka tela na kojem se naprezanje promatra. Takvo puno naprezanje je vektor generalno položen pod uglom prema normali na presek i može se rastaviti na tri skalarne komponente vezane uz koordinatni sistem: jednu u smeru normale x na presek (σ_x, normalno naprezanje) i dve na nju normalne koje leže u površini preseka u smeru preostale dve ose (τ_xy i τ_xz, tangencijalna ili smicaona naprezanja). Uzimajući svaku osu kao normalu na odgovarajući presek, proizlazi da u svakoj tački tela postoji devet komponenata naprezanja vezanih uz jedan koordinatni sistem, koje deluju na element zapremine i koje čine takozvani tenzor naprezanja drugoga reda. Zbog simetričnosti toga tenzora, koja sledi iz uslova ravnoteže elementa zapremine, samo je 6 međusobno različitih komponenata, jer je τ_ij = τ_ji (na primer τ_xy = τ_yx). Kako se u nekoj tački menja orijentacija koordinatnih osa, tako se menjaju i iznosi naprezanja. U svakoj tački tela moguća je takva orijentacija ose prema kojima postoje samo normalna naprezanja, dok su pomična jednaka nuli. Ta tri naprezanja nazivaju se glavnim naprezanjima, od kojih su dva ekstremne vrednosti σ_max i σ_min u toj tački.

Zbog unutarnjih silâ javljaju se u telu deformacije s kojima su naprezanja vezana preko Hukovog zakona. Čvrstoća konstruktivnih elemenata procenjuje se prema takozvanim hipotezama ili teorijama čvrstoće u kojima naprezanja imaju presudnu ulogu.

Deformacija

Glavni članak: Deformacija

Deformacija (lat. deformatio: izobličenje, nagrđivanje), u fizici, je promena oblika tela (rastezanje, savijanje, usukivanje i drugo) pod uticajem spoljašnjih ili unutarnjih sila. Može biti elastična, kada se nakon prestanka delovanja sile telo vraća u prvobitni oblik, i neelastična, kada deformisani oblik ostaje i nakon prestanka delovanja sile.

Dijagram naprezanja

Glavni članak: Dijagram naprezanja

Dijagram naprezanja prikazuje medusobnu zavisnost σ - zateznog naprezanja i ε - relativnog produženja ili linijske zatezne deformacije. U materijalu koji je opterećen nekom silom F nastaju naprezanja σ koja uzrokuju njegovo rastezanje. Naprezanje σ je odnos sile F i površine A preseka štapa ili šipke (normalnog na odnos sile).

$\sigma ={\frac {F}{A}}$

Zbog delovanja sile F (a time nastalog naprezanja σ) štap ili šipka će se od početne dužine L₀ rastegnuti na duljinu L. Tako je produženje štapa ili šipke:

$\varepsilon ={\frac {\Delta L}{L_{0}}}={\frac {L-L_{0}}{L_{0}}}$

Relativno produljenje ε (duljinska ili uzdužna deformacija) štapa ili šipke je produženje s obzirom na početnu dužinu L_o. Početno je naprezanje linearno (deformacija je direktno srazmerna naprezanju). U području linearnog rastezanja (Hukov zakon) materijal je elastičan i nakon prestanka delovanja sile, odnosno naprezanja, on se vraća u početno stanje. Jangov modul elastičnosti je odnos naprezanja i relativnog produženja (u području elastičnosti).

Tehnička granica elastičnosti je naprezanje pri kojem osetljivi instrumenti osete prvo primetno trajno produženje materijala (pri još nepromenjenom preseku A_o). Nakon te granice (obično na kraju linearnog rastezanja) materijal se rasteže plastično i nakon prestanka delovanja sile ne vraća se više na početnu dužinu L₀, već ostaje određeno trajno produženje, uz suženje preseka, A < A₀).

Geometrijska svojstva preseka

Moment inercije

Glavni članak: Moment inercije

Moment tromosti ili moment inercije (znak I ili J) je fizička veličina koja opisuje tromost ili inerciju čestice ili krutog tela pri promeni brzine ili smera vrtnje; jednaka je zbiru umnožaka mase m i kvadrata udaljenosti r od ose rotacije svake čestice koja čini telo:

$I=\sum _{i=1}^{N}m_{i}{r_{i}}^{2}$

Moment inercije nekog tela zavisi od oblika tela, raspodele mase, položaja ose rotacije. Na primer, ako je m masa tela, r njegov poluprečnik, a osa rotacije ujedno i osa simetrije, moment inercije na primer šupljeg valjka ili prstena iznosi:

$I=mr^{2}$

homogeno ispunjenog valjka ili kružne ploče:

$I={\frac {mr^{2}}{2}}\,\!$

homogeno ispunjene kugle:

$I={\frac {2mr^{2}}{5}}\,\!$

Moment inercije homogeno ispunjenog štapa kojemu je osa rotacije normalna na dužinu štapa nalazi se na polovini dužine štapa:

$I={\frac {mr^{2}}{12}}\,\!$

a na kraju je štapa:

$I={\frac {mr^{2}}{12}}\,\!$

gde je: r - dužina štapa. Merna je jedinica momenta inercije kilogram puta kvadratni metar (kg m²).

Naprezanje i deformiranje štapa

Na štapu kao modelu tela kojem je jedna mera ili dimenzija (dužina) znatno veća od druge dve postoje jednostavna opterećenja: rastezanje, uvijanje, savijanje, izvijanje i druga.

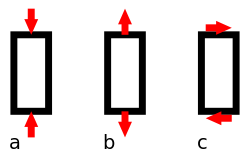
Istezanje i pritiskanje

Štap je osno ili aksijalno opterećen ako su u svakom preseku štapa sve komponente osim normalne sile (uzduž ose štapa) jednake nuli. U središnjem su delu naprezanja jednoliko raspodeljena i u njima naprezanje iznosi:

$\sigma ={\frac {F}{A}}$

gde je: F - normalna sila na štap, a A - površina poprečnog preseka štapa. Ako je dužina štapa mnogo veća od debljine (l / h > 10 - 20), može se uticaj odstupanja od jednolikog naprezanja u rubnom prelaznom području na produženje zanemariti. Tada je:

$\Delta l=\varepsilon \cdot L$

gde je: Δ l - promena dužine, a l - dužina štapa. Primenom Hukovog zakona izraz prelazi u:

$\Delta l={\frac {F}{E\cdot A}}\cdot l={\frac {\sigma }{E}}\cdot l$

gde je: E - Jangov modul elastičnosti.

Toplotna naprezanja

Toplotna naprezanja σ_T pojavljuju se pri zagreavanju ili hlađenju čvrsto fiksiranih predmeta:

$\sigma _{T}=E\cdot \varepsilon =E\cdot {\frac {\Delta l}{l}}$

gde je: Δ l - dužinsko ili linearno toplotno istezanje (ili skraćenje):

$\Delta l=\alpha _{L}\cdot l_{0}\cdot \Delta T$

gde je: l₀ - početna dužina, ΔT - temperaturna razlika, α_L - koeficijent toplotnog istezanja. Toplotna naprezanja upetog štapa proizlaze:

$\sigma _{T}=E\cdot \alpha _{L}\cdot \Delta T$

Toplotna naprezanja ne zavise od razmera predmeta i mogu biti katkada vrlo velika.

Uvijanje ili torzija

Glavni članak: Torzija

Uvijanje ili torzija (kasnolat. torsio: uvrtanje, uvijanje) je način opterećenja elementa konstrukcije kada oko neke njegove ose deluju dva jednaka i suprotno usmerena momenta (sprega). Tako su na primer opterećena vratila radnih mašina ili pogonske osovine vozila kada na njih sa jedne strane deluje pogonski moment, a sa druge otpor radnog dela mašine (na primer alata) ili točka vozila. Slično mogu biti opterećeni i stubovi nosećih metalnih konstrukcija (dizalica, građevina, dalekovoda i slično), koji su jednim krajem uklešteni u temelje, a na drugom stalno ili samo povremeno (udari vetra) deluje moment koji stub uvija oko njegove uzdužne osi. Elementi opterećeni na uvijanje pojednostavnjeno se prikazuju štapovima, a proračunima im se određuju deformacije (ugao uvijanja) i naprezanja (smicanje, ređe i normalna). Za ravne štapove poprečnog kružnog preseka ili preseka u obliku kružnog venca (na primer šuplje osovine) proračuni se sa visokom tačnošću sprovode uz pretpostavke da pri uvijanju poprečni preseci ostaju ravni i normalni na uzdužnu osu štapa, da se preseci zakreću kao krute figure (poluprečnici pri zakretanju ostaju ravni) te da se na presecima ne javljaju normalna naprezanja. U središtu preseka takvog štapa pomično naprezanje jednako je nuli, a na vanjskom rubu preseka, poluprečnika r, ono ima maksimalnu vrednost:

$\tau ={\frac {M_{t}\cdot r}{I_{p}}}$

gde je: M_t - moment torzije ili uvijanja, a I_p polarni moment inercije površine preseka u odnosu na središte, koji za puni presek iznosi:

$I_{p}={\frac {\pi \cdot r^{4}}{2}}$

a za kružni venac, unutarnjeg i spoljašnjeg polupreseka r i R:

$I_{p}={\frac {\pi \cdot (R^{4}-r^{4})}{2}}$

Kod toga će se krajnji preseci štapa dužine l i modula smicanja G, koji zavisi samo od vrste materijala štapa, zakrenuti jedan u odnosu na drugog za ugao

$\phi _{}={M_{t}\cdot l \over I_{p}\cdot G}$

Kod uvijanja neokruglih štapova poprečni se preseci iskrivljuju, navedene pretpostavke više ne vrede, a proračuni pomičnih naprezanja i deformacija su složeniji. U granicama Hukovog zakona moment torzije M_t i ugao zakreta φ međusobno su proporcionalni, tako da vredi:

$M_{t}=D\cdot \phi$

D je takozvani direkcijski moment (torzijska krutost) sa jedinicom Nm/rad, koji za štap punog kružnog preseka ili kružnoga venca iznosi G Ip / l.

Savijanje

Glavni članak: Savijanje

Za razliku od osnog opterećenja (istezanje i pritisak), pri savijanju štapa deformiše se uzdužna osa štapa. Deformisana uzdužna osa zove se elastična linija ili progib. Razlikuje se čisto savijanje i poprečno savijanje. Pri čistom savijanju sve su komponente unutrašnjih sila jednake nuli, osim momenta savijanja. Pri poprečnom savijanju osim momenta savijanja pojavljuje se još i poprečna sila koja uzrokuje smicanje. Čisto savijanje zove se još i savijanje spregovima, a poprečno savijanje, savijanje silama. Moment savijanja uzrokuje normalna naprezanja σ koja se zamišljaju razdeljenima po preseku srazmerno udaljenosti od neutralne ose. Neutralna osa prolazi kroz težište promatranog preseka. Klasična jednakost koja određuje naprezanje u gredi usled delovanja čistog savijanja je:

${\sigma }={\frac {M\cdot y}{I_{x}}}$

gde je: ${\sigma }$ - naprezanje usled savijanja, M - moment savijanja oko neutralne ose x, y - normalna udaljenost od neutralne ose x, I_x - momenat inercije ili momenat tromosti oko neutralne ose x.

Maksimalno naprezanje na savijanje σ_max pojavljuje se u tački koja je najudaljenija od neutralne ose y_max:

$\sigma _{max}={\frac {M\cdot y_{max}}{I_{x}}}={\frac {M}{W_{x}}}$

gde je: ${W_{x}}$ - moment otpora preseka.

Progib nosača ${\delta }$ proizlazi iz diferencijalne jednakosti elastične linije:

${\delta }={\frac {M_{x}}{E\cdot I_{x}}}$

Uobičajene vrednosti za maksimalne momente savijanja, progibe, momente tromosti i momente otpora preseka date su u tablicama.

Smicanje

Glavni članak: Smicanje

Smicanje, smik, posmik ili odrez je opterećenje čvrstog tela silama koje deluju u ravni nekog preseka tela, a nastoje da izazovu paralelno klizanje jednog dela preseka (tankoga sloja) u odnosu na drugi. Tako su na primer opterećene zakovice koje spajaju krajeve metalne trake u obruč, kada duž obruča deluju zatezne sile. Jednako tako, kod torzije (uvijanja) štapa okruglog preseka momentima (na primer vratilo), preseci normalni na uzdužnu osu štapa napregnuti su na smicanje. Smično opterećenje koristi se u nekim tehnološkim postupcima, kao što je na primer rezanje makazama, probijanje štancanjem i drugo. U elementima konstrukcija smicanje se najčešće javlja zajedno sa savijanjem. Posledica su smicanja reaktivna smicaona (tangencijalna) naprezanja τ koja leže u ravni preseka tela, a raspodeljena su po nekom zakonu zavisno od načina delovanja sila i momenata. Tako su kod savijanja štapova silama naprezanja raspodeljena parabolično, kod uvijanja linearno i tako dalje. U opštem slučaju opterećenja, na svaki beskonačno mali element površine deluju, osim normalnih, i smicaona naprezanja, koja čine spregove. Pod delovanjem tih spregova dolazi do promene prvotno pravog ugla između dve međusobno normalne stranice elementa za mali ugao γ (ugaona deformacija), koji meren u radijanima kod elastičnih deformacija iznosi:

$\gamma ={\tau \over G},$

gde je: G - modul smicanja zavistan od materijala (sprega sila).

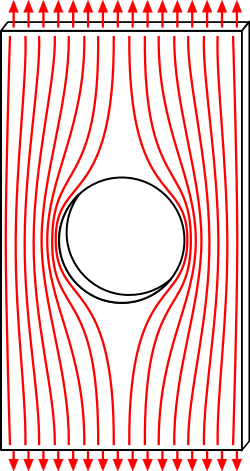
Izvijanje

Glavni članak: Izvijanje

Izvijanje je gubitak stabilnosti štapa ili nekog drugog vitkog elementa konstrukcije osno opterećenog prekomerno velikom pritisno silom. Tako se na primer štap, postavljen normalno na tlo i odozgo pritisnut pritisnom silom, izvije (izboči) u trenutku kada se sila poveća preko određene granice (Ojlerova kritična sila). Rešetkaste konstrukcije koje su sastavljene od štapova (stubovi dalekovoda, čelični mostovi, dizalice) obično gube stabilnost zbog izvijanja jednog ili više štapova, pa se u proračunima takvih konstrukcija posebna pažnja posvećuje pritisno najopterećenijim štapovima. Intenzitet kritične sile pri kojem nastaje izvijanje zavisi od vitkosti štapa, to jest načina učvršćenja njegovih krajeva i njegovim geometrijskim svojstvima, te o mehaničkim svojstvima materijala od kojeg je štap načinjen. Kod konstrukcija sa pločama i ljuskastim elementima izvijanje je složenije. Kritičnom silom bavio se švajcarski matematičar, fizičar i astronom Leonard Ojler, po kojem je ta sila i nazvana.

Literatura

• Fa-Hwa Cheng, Initials. (1997). Strength of material. Ohio: McGraw-Hill
• Mechanics of Materials, E.J. Hearn
• Alfirević, Ivo. Strength of Materials I. Tehnička knjiga. 1995. ISBN 978-953-172-010-6..
• Alfirević, Ivo. Strength of Materials II. Tehnička knjiga. 1999. ISBN 978-953-6168-85-9..
• Ashby, M.F. Materials Selection in Design. Pergamon, 1992.
• Beer, F.P., E.R. Johnston, et al. Mechanics of Materials, McGraw-Hill. (3rd изд.). 2001. ISBN 978-0-07-248673-5. 
• Cottrell, A.H. Mechanical Properties of Matter. Wiley, New York, 1964.
• Den Hartog, Jacob P. Strength of Materials. Dover Publications, Inc. 1961. ISBN 978-0-486-60755-9..
• Drucker, D.C. Introduction to Mechanics of Deformable Solids. McGraw-Hill, 1967.
• Gordon, J.E. The New Science of Strong Materials. Princeton, 1984.
• Groover, Mikell P. Fundamentals of Modern Manufacturing, John Wiley & Sons,Inc. (2nd изд.). 2002. ISBN 978-0-471-40051-6. .
• Hashemi, Javad and William F. Smith. Foundations of Materials Science and Engineering, McGraw-Hill. (4th изд.). 2006. ISBN 978-0-07-125690-2. .
• Hibbeler, R.C. Statics and Mechanics of Materials, SI Edition. Prentice-Hall. 2004. ISBN 978-0-13-129011-2..
• Lebedev, Leonid P. and Michael J. Cloud. Approximating Perfection: A Mathematician's Journey into the World of Mechanics. Princeton University Press. 2004. ISBN 978-0-691-11726-3..
• Gent, A.N.; Mars, W.V. (2013). „Strength of Elastomers”. Ур.: James E. Mark; Burak Erman; Mike Roland. The Science and Technology of Rubber (4th изд.). стр. 473—516. ISBN 9780123945846. doi:10.1016/B978-0-12-394584-6.00010-8. 
• Mott, Robert L. Applied Strength of Materials, Prentice-Hall. (4th изд.). 2002. ISBN 978-0-13-088578-4. .
• Popov, Egor P. Engineering Mechanics of Solids. Prentice Hall, Englewood Cliffs, N. J. 1990. ISBN 978-0-13-279258-5..
• Ramamrutham, S. Strength of Materials.
• Shames, I.H. and F.A. Cozzarelli. Elastic and inelastic stress analysis. Prentice-Hall. 1991. ISBN 978-1-56032-686-1..
• Timoshenko S. Strength of Materials, Krieger Publishing Company. (3rd изд.). 1976. ISBN 978-0-88275-420-8. .
• Timoshenko, S.P. and D.H. Young. Elements of Strength of Materials, 5th edition. (MKS System)
• Davidge, R.W., Mechanical Behavior of Ceramics, Cambridge Solid State Science Series, (1979)
• Lawn, B.R., Fracture of Brittle Solids, Cambridge Solid State Science Series, 2nd Edn. (1993)
• Green, D., An Introduction to the Mechanical Properties of Ceramics, Cambridge Solid State Science Series, Eds. Clarke, D.R., Suresh, S., Ward, I.M.Babu Tom.K (1998)

Spoljašnje veze

• Failure theories
• Case studies in structural failure